

Cable Info
The coaxial cables
this page you will find some informations about some coaxial cables which may be usefull for you.
Generalities
Properties of dielectricals used in coaxial cables
Properties of some coaxial cables
Links to some coaxial manufacturers

Generalities
Velocity of Propagation
When an electromagnetic wave travels in a medium other than air or vacuum, the velocity for the wave is reduced by a factor of the square root
of the dielectric constant of the media. The velocity (v) of the propagation of a signal is given by the formula :
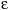

Where c is the speed of light, 3 x 108 m/sec or 1.18 x 1010 in/sec, and is the dielectric constant of the medium.
The wavelength of a signal is given by the formula:
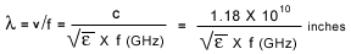
Attenuation
A wave loses energy (attenuates) in several ways:
1.
The resistance of the inner and outer conductors is small but can be significant over long lengths and will produce some heat.
2.
The dielectric may cause loss; it's resistance is high but not infinite, and some energy is lost.
3.
Electromagnetic energy radiates at high frequencies; significant energy losses are caused by radiation of electromagnetic energy (the
cable acts like an antenna).
4.
Energy is reflected due to impedance mismatches or impedance discontinuities. The combination of these four types of losses are
referred to as the insertion loss of a transmission line system.
Characteristic Impedance
A parameter which defines the behavior of a cable, connector, or any propagating system.
The characteristic impedance Zo of a lossless cable is related to the inductance per unit length, L, and the capacitance per unit length, C, as
follows:
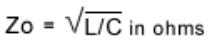
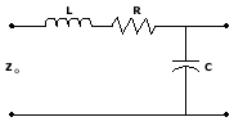
The equivalent circuit of a transmission line is shown in Figure 4. R represents the conductor resistance for a unit length.
For a coaxial cable the characteristic impedance is given by:
Figure 4
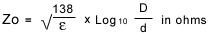
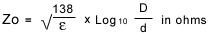
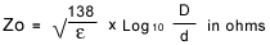
where "D" is the inner diameter of the outer conductor and "d" is the outer diameter of the inner conductor, respectively. Similar equations
apply for other geometries such as two parallel wires.
As can be observed from this equation, the impedance is a function of the diameters. Generally the conductor diameter can be very accurately
controlled, but the dielectric diameter can vary based on the accuracy of the process. If the impedance changes are a consistent spacing of one
1/4 wavelength, this can cause signifigant signal loss.
Reflections
When the characteristic impedance changes in a transmission line system, part of an incident wave is reflected. The reflection coefficient can be
calculated as:
Where Vi and Zo are the incident voltage and impedance of the first media. VR and ZR represent the reflected voltage and impedance of the
media that caused the reflection. The decibel loss due to reflection is given by:
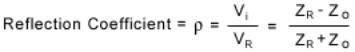
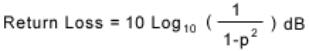
VSWR
The traditional way to determine the reflection coefficient is to measure the standing wave caused by the superposition of the incident wave
and the reflected wave. Traditionally the voltage is measured at a series of points using a slotted line. The ratio of the maximum divided by the
minimum is the Voltage Standing Wave Ratio (VSWR). The VSWR is infinite for total reflections because the minimum voltage is zero. If no
reflection occurs the VSWR is 1.0. VSWR and reflection coefficient are related as follows:
Present instrumentation measures the return loss.
Figure 5 represents the relationship between VSWR and its equivalent in return loss (expressed in dB).
If there is a series of impedance changes, each one will cause a reflection. The total reflection is the vector addition of each of the individual
coefficients accounting for the distance between discontinuities. Even though the calculations are difficult, a total VSWR can still be measured.
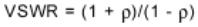
Properties of different dielectrics
Multiple Reflections

Properties of some coaxial cables

DH1RK
Navigate
Navigate



- FK310 AntennaTuner
- Setup 2008
- Inverted L - Simulation
- Inverted L - Installation
- Inverted L - Matching
- SteppIR - Simulation / 20m band
- SteppIR - Simulation / 17m band
- SteppIR - Simulation / 15m band
- SteppIR - Simulation / 12m band
- SteppIR - Simulation / 10m band
- SteppIR - Simulation / 6m band
- SteppIR - Simulation Overview
- SteppIR - Installation
- HighBands -Yagis
- HighBands -Groundplanes
- Setup 2005





















